There are three essential theorems that capture the fundamentals of multivariable calculus. (And no, I'm not referring to the fundamental theorem of calculus. That's far to simple!)
1. Green's Theorem
Green's theorem essentially says that you can take any positively oriented closed curve in the plane and rewrite it as a double integral over the area enclosed by the curve. In other words:
2. Divergence Theorem
The divergence theorem says that you can take any non-closed surface, S, in space with a boundary, C, and describe the flux across the surface as a triple integral of the divergence in the volume enclosed by the surface.
3. Stokes' Theorem
And to wrap everything together, Stokes' Theorem says that a loop integral on the boundary, C, of a non-closed surface, S, can be rewritten as a double integral of the curl of a vector field, F, across the surface.
These three theorems can be said to be "fundamental" because they relate the boundaries of surfaces to the interior of those surfaces, just as in basic calculus, the "interior" of a one-dimensional curve in the plane can be related to the endpoints of that curve.
Thursday, June 7, 2012
Sunday, May 27, 2012
Parametric Surfaces
How do you turn a one-dimensional vector-valued function r(t) into two-dimensional surface? Rhetorically, that's like asking how to turn f(x) into f(x,y)--you just add another variable. But instead of making the vector function r(t,z), the conventional form is r(u,v).
For instance, take <cos(u), sin(u), v>, where u ranges from 0 to 2pi and v ranges from 0 to 3. The x- and y-components dictate that in the xy-plane, you have a circle. And what does that circle do? It gets extruded upwards to 3. The end result is a cylinder with radius 1 and height 3.
What is the purpose of having another way to describe a surface? The primary reason is because the function is easier to interpret.
In the 2D plane, we're familiar with:
For instance, take <cos(u), sin(u), v>, where u ranges from 0 to 2pi and v ranges from 0 to 3. The x- and y-components dictate that in the xy-plane, you have a circle. And what does that circle do? It gets extruded upwards to 3. The end result is a cylinder with radius 1 and height 3.
What is the purpose of having another way to describe a surface? The primary reason is because the function is easier to interpret.
In the 2D plane, we're familiar with:
as a circle of radius 3. But in 3-space, that becomes a cylinder. But what's to distinguish one from another? In parametric, however, this difference is clear.
Thursday, May 17, 2012
Hyperbolic Trig Functions
And just when you thought that you were rid of them for the rest of your math career, they're back (with a vengeance)! Well...not quite. We should all be familiar with the family of trigonometric functions: sine, cosine, tangent, secant, co-secant, and co-tangent. And we shouldn't forget all of their lovely derivatives. And the derivatives of their inverse functions. Well, don't fret when I tell you that there's more.
Hyperbolic trig functions are a separate class of functions that look like sines and cosines, and similarly, also have somewhat familiar derivatives and other properties. For instance, take sinh (x), the hyperbolic sine
function, pronounced "sin-sh". Though it is defined as:
it's derivative, like sin (x) is just what you'd think: cosh (x), the hyperbolic cosine, pronounced "cosh". But what's interesting is that the derivative of cosh (x), defined as:
isn't -sinh (x), like how the derivative of cos(x) is -sin(x). Rather, it's just sinh(x). So the sinh(x) and cosh(x) have cyclic derivatives!
Some other "look alike" derivatives of hyperbolic trig functions include:
Hyperbolic trig functions are a separate class of functions that look like sines and cosines, and similarly, also have somewhat familiar derivatives and other properties. For instance, take sinh (x), the hyperbolic sine
function, pronounced "sin-sh". Though it is defined as:
it's derivative, like sin (x) is just what you'd think: cosh (x), the hyperbolic cosine, pronounced "cosh". But what's interesting is that the derivative of cosh (x), defined as:
isn't -sinh (x), like how the derivative of cos(x) is -sin(x). Rather, it's just sinh(x). So the sinh(x) and cosh(x) have cyclic derivatives!
Some other "look alike" derivatives of hyperbolic trig functions include:
As of yet, I haven't noticed any pattern to help memorize which derivatives are "mirror-images" of each other, but if anyone does discover something, drop a comment!
Sunday, April 29, 2012
Line Integrals
Line integrals calculate summations of some quantifiable object X (for instance, density) over a path. We discussed in class how line integrals can also apply to paths that turn and go around in space. To calculate such integrals, we simply need to describe the path as a piece-wise function and integrate accordingly.
 In one of our problems, we reversed the path our particle in our line integral would take and we got the exact opposite answer. But what if instead of reversing the path, we reversed the vector field? The answer we arrived at was that it would not yield the same answer. The reversed vector field wouldn't affect the path that the particle took in the same way.
In one of our problems, we reversed the path our particle in our line integral would take and we got the exact opposite answer. But what if instead of reversing the path, we reversed the vector field? The answer we arrived at was that it would not yield the same answer. The reversed vector field wouldn't affect the path that the particle took in the same way.
If you look closely, the angle between the original vector field and the tangent to the curve is slightly larger than that of the reversed vector field. So reversing a vector field won't necessarily generate the opposite amount of net work done by the particle, but does yield some interesting phenomenon in physics.
For instance, if you shatter a glass, every resulting shard has a force vector pointing outwards from the origin of, shall we say, collapse? Well, what if we reversed all those vectors? Would the glass come back together? (Link below)
Skip to around 6 seconds and imagine freezing a glass that had just shattered and reversing all those force vectors. And perhaps this would happen.
It's definitely an interesting thing to picture in your head!
 In one of our problems, we reversed the path our particle in our line integral would take and we got the exact opposite answer. But what if instead of reversing the path, we reversed the vector field? The answer we arrived at was that it would not yield the same answer. The reversed vector field wouldn't affect the path that the particle took in the same way.
In one of our problems, we reversed the path our particle in our line integral would take and we got the exact opposite answer. But what if instead of reversing the path, we reversed the vector field? The answer we arrived at was that it would not yield the same answer. The reversed vector field wouldn't affect the path that the particle took in the same way.If you look closely, the angle between the original vector field and the tangent to the curve is slightly larger than that of the reversed vector field. So reversing a vector field won't necessarily generate the opposite amount of net work done by the particle, but does yield some interesting phenomenon in physics.
For instance, if you shatter a glass, every resulting shard has a force vector pointing outwards from the origin of, shall we say, collapse? Well, what if we reversed all those vectors? Would the glass come back together? (Link below)
Skip to around 6 seconds and imagine freezing a glass that had just shattered and reversing all those force vectors. And perhaps this would happen.
It's definitely an interesting thing to picture in your head!
Thursday, April 26, 2012
Vector Fields - Conservative Fields in Space
As it turns out, determining whether or not a vector field is conservative in space is radically different than that of a vector field in the plane. To determine whether or not a vector field is conservative in space (and by this, I mean 3D vector fields), we need to take the cross product of the gradient and our vector function. This yields a matrix:
This is called the curl of vector field F. If the curl is the zero vector, then the vector field is conservative.
Wednesday, April 18, 2012
Vector Fields - Conservative Fields in Planes
Recall that from the typical functions that we are familiar with, we have "continuous" and "discontinuous" functions. The well-behaved functions are called "continuous." In the case of vector fields, well-behaved fields are termed conservative.
A vector field is mathematically defined as conservative if and only if it exists as the gradient of another function, called the potential function. In other words:
But this doesn't mean that given some vector field, you absolutely must engage in complicated mathematics to determine whether or not it supports abortion. Take for instance:
We know that if this is the gradient of some function, it is conservative. The "i" component of the vector is the partial derivative with respect to x; likewise, the "j" component is the partial derivative with respect to y. Easily enough, we can see that the following function indeed works:
But what if we wanted a more reliable method of confirming this? The following would do just that. Consider this general vector formula:
That vector is conservative if:
And why does this make sense? If the vector field "F" is the gradient of some potential function, then it should be in this format:
If this function is "well-behaved", then its mixed partials should be equal. Thus, we arrive at our conservative formula.
Now, this process gets radically different in three-dimensions, but it isn't all that bad. But lets leave that for another post and another time.
Happy vector conserving!
A vector field is mathematically defined as conservative if and only if it exists as the gradient of another function, called the potential function. In other words:
We know that if this is the gradient of some function, it is conservative. The "i" component of the vector is the partial derivative with respect to x; likewise, the "j" component is the partial derivative with respect to y. Easily enough, we can see that the following function indeed works:
But what if we wanted a more reliable method of confirming this? The following would do just that. Consider this general vector formula:
That vector is conservative if:
If this function is "well-behaved", then its mixed partials should be equal. Thus, we arrive at our conservative formula.
Now, this process gets radically different in three-dimensions, but it isn't all that bad. But lets leave that for another post and another time.
Happy vector conserving!
Tuesday, April 17, 2012
Vector Fields - Introduction & Basics
We continued our discussion on vector fields in class today. Essentially, a vector field is simply another function, which we are familiar with.
Rectangular functions of two variables takes an x-coordinate as an input and outputs a y-coordinate (or vice versa). Three variable rectangular functions take a point in the plane (both x and y) and outputs a point in space (associating a z-coordinate). Vector valued functions take x-values and output vectors.
Finally, vector fields take in points (both x and y), and output vectors.
Keep in mind that vector fields cover the entire domain of the plane, or space, depending on how many dimensions you are working with. In class, we graphed and analyzed some basic vector fields, associating them with some natural phenomena.
1.
The most basic one: v (x,y) = <x , y> is described as consisting of vectors pointing radially outwards with magnitudes proportional to its distance from the origin. We associated it with the "Big Bang," as the universe's expansion is supposedly accelerating.
2.
The reverse of this vector field: v (x,y) = <-x , -y> essentially reverses every vector in the field. We described the resulting field as the opposite of the Big Bang, or the "Big Crunch."
3.
Our third basic vector field looks a little more natural. We associated the field described by: v (x,y) = <y , x> with two water currents colliding with each other. Note that the reverse vector: v (x,y) = <-y , -x> would just have the "entrance" and "exit" of the vectors reversed.
4.
And finally, our favorite of the day, the "Toilet Flush": v (x,y) = <y , -x>. The reverse of this function: v (x,y) = <-y , x> would simply be a toilet being flushed on the other side of the world.
The drawings I added to go with the vector fields aren't entirely correct, but it's just there to give a less cluttered visualization.
To draw your own vector fields, just plot a few vectors at various points in the plane and try to see a pattern. They're usually symmetric, whether it's about the origin in the case of the "toilet flush" or about the lines y = x and y = -x in the case of "water currents".
Happy...vector field-ing?
Rectangular functions of two variables takes an x-coordinate as an input and outputs a y-coordinate (or vice versa). Three variable rectangular functions take a point in the plane (both x and y) and outputs a point in space (associating a z-coordinate). Vector valued functions take x-values and output vectors.
Finally, vector fields take in points (both x and y), and output vectors.
Keep in mind that vector fields cover the entire domain of the plane, or space, depending on how many dimensions you are working with. In class, we graphed and analyzed some basic vector fields, associating them with some natural phenomena.
1.
The most basic one: v (x,y) = <x , y> is described as consisting of vectors pointing radially outwards with magnitudes proportional to its distance from the origin. We associated it with the "Big Bang," as the universe's expansion is supposedly accelerating.
2.
The reverse of this vector field: v (x,y) = <-x , -y> essentially reverses every vector in the field. We described the resulting field as the opposite of the Big Bang, or the "Big Crunch."
3.
Our third basic vector field looks a little more natural. We associated the field described by: v (x,y) = <y , x> with two water currents colliding with each other. Note that the reverse vector: v (x,y) = <-y , -x> would just have the "entrance" and "exit" of the vectors reversed.
4.
And finally, our favorite of the day, the "Toilet Flush": v (x,y) = <y , -x>. The reverse of this function: v (x,y) = <-y , x> would simply be a toilet being flushed on the other side of the world.
The drawings I added to go with the vector fields aren't entirely correct, but it's just there to give a less cluttered visualization.
To draw your own vector fields, just plot a few vectors at various points in the plane and try to see a pattern. They're usually symmetric, whether it's about the origin in the case of the "toilet flush" or about the lines y = x and y = -x in the case of "water currents".
Happy...vector field-ing?
Monday, April 16, 2012
Multiple Integration - Spherical Coordinates
Sorry for the late post (haven't gotten around to updating the blog over spring break)!
But yes, it's another coordinate system. Just as with cylindrical coordinates mentioned in the last post, spherical is somewhat of a cousin of our old polar coordinates.
(Refer to the blog archive for a refresher on polar coordinates.)
There are three components to coordinatizing points in spherical:
Both "rho" and "theta" are exactly the same as polar and cylindrical. The only difference between spherical and cylindrical, however, is the final component. This difference makes sense, though. Take a moment and imagine a cylinder. It is, in essence, a circle extruded infinitely in the z-direction. Therefore, it only makes sense for it to have a z-component to its point-coordinates. For a sphere, however, you have "phi", the extent of the surface from the positive z-axis.
Imagine a circle on the yz-plane extruded down to the xy-plane as depicted in the image below. If the top of the circle is only brought down to the xy-plane, it has only completed 1/4 of its way around the coordinate plane, so "phi" is pi/4. Keep in mind, however, that since "phi" is only measured from the positive z-axis, the highest possible value for "phi" is pi. This prevents doubling-over when measuring "phi".
To integrate, simply keep the following conversions from rectangular to spherical in mind and integrate accordingly:
Also, just as with cylindrical coordinates, there is a new "dV" in spherical, which may seem a little daunting at first sight, but isn't that bad once the trigonometric functions eliminate the angles involved with "theta" and "phi":
A short sample:
Consider the following sphere of radius 4 (it looks like a cracked egg, but bear with me):
Let's write the triple integral that will result in it's enclosed volume.
It may seem a little confusing at first, but with a little practice, it'll get easier.
Happy spherical integrating!
But yes, it's another coordinate system. Just as with cylindrical coordinates mentioned in the last post, spherical is somewhat of a cousin of our old polar coordinates.
(Refer to the blog archive for a refresher on polar coordinates.)
There are three components to coordinatizing points in spherical:
Both "rho" and "theta" are exactly the same as polar and cylindrical. The only difference between spherical and cylindrical, however, is the final component. This difference makes sense, though. Take a moment and imagine a cylinder. It is, in essence, a circle extruded infinitely in the z-direction. Therefore, it only makes sense for it to have a z-component to its point-coordinates. For a sphere, however, you have "phi", the extent of the surface from the positive z-axis.
Imagine a circle on the yz-plane extruded down to the xy-plane as depicted in the image below. If the top of the circle is only brought down to the xy-plane, it has only completed 1/4 of its way around the coordinate plane, so "phi" is pi/4. Keep in mind, however, that since "phi" is only measured from the positive z-axis, the highest possible value for "phi" is pi. This prevents doubling-over when measuring "phi".
To integrate, simply keep the following conversions from rectangular to spherical in mind and integrate accordingly:
Also, just as with cylindrical coordinates, there is a new "dV" in spherical, which may seem a little daunting at first sight, but isn't that bad once the trigonometric functions eliminate the angles involved with "theta" and "phi":
A short sample:
Consider the following sphere of radius 4 (it looks like a cracked egg, but bear with me):
- It extends from the positive z-axis to the negative z-axis, so "phi" is pi.
- It extends all the way around the xy-plane, so "theta" is two-pi.
- And it's radius is 4, so "rho" is 4.
It may seem a little confusing at first, but with a little practice, it'll get easier.
Happy spherical integrating!
Wednesday, April 4, 2012
Multiple Integration - Cylindrical Coordinates
Having new coordinate systems to work with may seem at first like an excess of information, but in some cases in mathematics, having another coordinate system to work with can actually make a difficult problem much easier.
Imagine cylindrical coordinates as the polar plane extruded along the z-axis. (Infinitely up and down). By this logic, the three components of cylindrical coordinates are:

This z-component makes all the difference. In polar coordinates, r=3 yields a circle with radius 3. In cylindrical, you get exactly what its name implies—a cylinder of radius 3. It's the circle we had in polar extruded infinitely in the z-direction.
But how do we integrate in cylindrical? Similar to how when we converted our dA or dV in rectangular integration to polar, we get an r with our differentials, in cylindrical integration, we get:
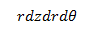 Simply express "theta" and the radius (r) as you would in polar. But now, you simply include the z-range and integrate the function accordingly.
Simply express "theta" and the radius (r) as you would in polar. But now, you simply include the z-range and integrate the function accordingly.To convert between rectangular and cylindrical, refer to the conversions mentioned in the March post: "Multiple Integration - Double w/ Polar".
Happy integrating in cylindrical!
Center of Mass - Double and Triple Integration
All this integrating can be tied together in center of mass. Imagine you have a cube that's gets denser as you move further out towards its corners. Where would it's "center of mass" or "core" be? That can be easily accomplished using multiple integration!
- If it's a 2D surface, use a double integral.
- If it's a 3D volume, use a triple integral.
To describe "x ranges" and "y ranges" for centers of mass, these ranges are described as "moments"--how the object acts in a certain direction, literally, at a certain moment in time. The general formulas for these are different for 2D and 3D objects. But the rules are somewhat similar.
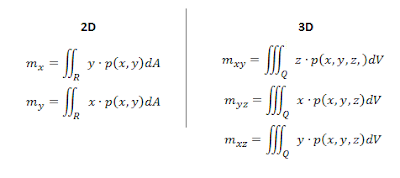 Notice that the main difference here is that instead of just having the surface vary along two axes, in 3D space, the object can vary along planes. Also, notice how within the integral, the function of density p(x,y,z) is being multiplied by an additional variable (either x, y, or z). Conveniently, by dividing these moments by the mass, you get one component of the center of mass. Put the components together and you'll get the coordinate of the center of mass for that particular surface or solid!
Notice that the main difference here is that instead of just having the surface vary along two axes, in 3D space, the object can vary along planes. Also, notice how within the integral, the function of density p(x,y,z) is being multiplied by an additional variable (either x, y, or z). Conveniently, by dividing these moments by the mass, you get one component of the center of mass. Put the components together and you'll get the coordinate of the center of mass for that particular surface or solid!Tuesday, April 3, 2012
Multiple Integration - Triple
Triple integration may seem like you're just sticking another integral sign onto a double integral, but it comes with its own set of complications. Similar to how in double integration, you could reverse the order of integration (either dydx or dxdy), in triple integration, you have an array of six possible orders to integrate. For this reason, it is imperative to sketch surfaces properly and keep your limits of integration organized. For instance, suppose you have the plane x + y + z = 1 in the first octant.
- Well, the range for x is easy: from 0 to 1.
- While x ranges from 0 to 1, y ranges from 0 to the line y=x, so from 0 to x.
- And while y ranges from 0 to x, z ranges from 0 to the plane, so from 0 to 1-x-y.
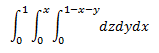
Now what if we switched the order of integration to dxdydz? Well, now we look at z first, then y, then x last.
- Z ranges from 0 to 1.
- This is where the change comes in. As z varies, y doesn't go out to the plane because our "depth" here is the x-coordinate and we haven't described that yet. To determine the limits on the y-axis, we have to look at the trace of the plane.
Remember that order matters!
Happy triple integrating!
Tuesday, March 27, 2012
Multiple Integration - Double w/ Polar
There are many things that can complicate the process of integration. For instance, what makes the first of the following integrals more daunting than the second?
 Well, you wouldn't be wrong if you said the square root. However, when we deal with circular regions, we have no choice but the work with square roots. But what if we could make our lives simpler by moving to another coordinate system--namely, polar? As it turns out, polar makes integrating circular regions that seem overly complicated in rectangular coordinates seem trivial!
Well, you wouldn't be wrong if you said the square root. However, when we deal with circular regions, we have no choice but the work with square roots. But what if we could make our lives simpler by moving to another coordinate system--namely, polar? As it turns out, polar makes integrating circular regions that seem overly complicated in rectangular coordinates seem trivial!But first, it's essential to keep some basic rectangular to polar conversions in mind:
Now, remember our general formula for double integrals?
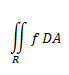 The DA in polar becomes not dydx, like in rectangular coordinates, because the x and y axes only exist in rectangular. In polar, we describe curves by their angle and radius! That's why in polar...
The DA in polar becomes not dydx, like in rectangular coordinates, because the x and y axes only exist in rectangular. In polar, we describe curves by their angle and radius! That's why in polar...So as a quick example, lets say we're trying to find the volume of the paraboloid x^2+y^2 = z over this circle:
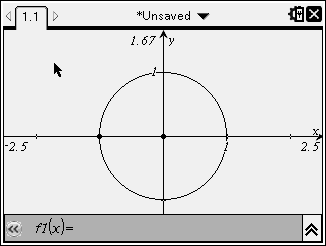 Well, we can establish the limits of integration of our area by describing the angle and the radius. The circle runs all the way around, so it extends from 0 to 2pi. The radius is 1.
Well, we can establish the limits of integration of our area by describing the angle and the radius. The circle runs all the way around, so it extends from 0 to 2pi. The radius is 1.Note: Double integration for polar coordinates puts the angle first, then the radius.
So our integral would look like:
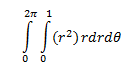
Remember that you also need to convert the equation of the paraboloid (x^2 + y^2) to polar as well, and then tack on the DA.
Happy polar integrating!
Wednesday, March 14, 2012
Multiple Integration - Double
Before multivariate calculus, many of us should have learned integration in two-dimensions, which essentially finds the area under a curve, constrained by certain limits. In three-dimensions, it's not the area under a curve we want, but rather, the volume. Therefore, it's only natural to think that we'd need a second integral to make it 3D. Below, you can see the general formula for a double integral:
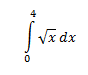 And that would yield the correct answer. However, we can express this as a double integral by "un-evaluating" the function. To do this, simply describe the region in terms of x and y.
And that would yield the correct answer. However, we can express this as a double integral by "un-evaluating" the function. To do this, simply describe the region in terms of x and y.- X ranges from 0 to 4
- Y ranges from 0 to sqrt x.
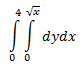 Now, this may seem trivial--why would anyone want to complicate an integral further by adding another one? Well, what if you were asked to find the volume under a curve over a certain area in the plane? As it turns out, double integrals make this very easy. For instance, the following curve over the adjacent area:
Now, this may seem trivial--why would anyone want to complicate an integral further by adding another one? Well, what if you were asked to find the volume under a curve over a certain area in the plane? As it turns out, double integrals make this very easy. For instance, the following curve over the adjacent area: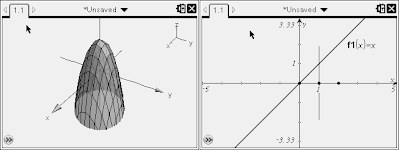 Simply describe the area of integration: x ranges from 0 to 1; y ranges from 0 to x, and double-integrate the paraboloid of x^2 + y^2 according to those limits dydx to get your answer!
Simply describe the area of integration: x ranges from 0 to 1; y ranges from 0 to x, and double-integrate the paraboloid of x^2 + y^2 according to those limits dydx to get your answer!Sunday, February 12, 2012
Tree Searching - Class Presentation
Tree searching is essentially a method of getting from point A to point B. There are two ways to conduct a tree search: one way generates many different results at once while another locates information related to one node first. This seems confusing, but please bear with the text till the end and things may become clearer to you.
Depth-first Searching: this search method basically takes your search through a tree as far in as possible. If there aren't any "priorities", the depth first search will mindlessly delve deeper and deeper until it hits a dead end. In the picture that follows, there is a comparison of the depth-first and breadth-first search method. Take note of how even though Node A branches into several other nodes, the search only returns to it after it has reached a deadend.
Breadth-first Search: contrary to a depth-first search which ignores all other branches from a node and returns them later, a breadth-first search explores all branches from one node before moving on to another, in order of priority if such exists. Again, note the image comparing the two search methods.
(Click to see image in full-size)
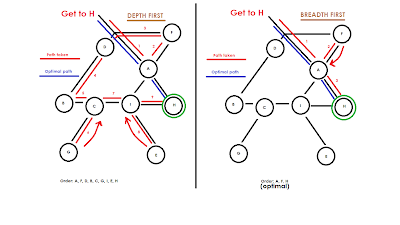
A possible application for this would be an automated maze generator/solver. Both work in essentially the same way. The program would simply randomly generate paths in a random direction and if i collides with terrain (computer limits), it will return to its previous starting point and generate in a different direction. For the maze solver, the program would explore the path uniformly until it hits a deadend and returns to the last split-point and explore the other way. In terms of mazes, the optimal search method for a solution would be the breadth-first search. Logically this makes sense because if the program chooses the wrong path, it will return to that node quicker and wind up on the right path than if it had been utilizing a depth-first search, in which case it would end up far deeper in the wrong direcion before it turns around.
This is a relatively interesting way of applying optimization that involves no calculus. In terms of mazes, we usually conduct our own breadth-first seach in our heads, mentally scanning the maze for possible dead ends and avoiding them. So get out those pencils and thinking caps!
Here's a link to an online program that demonstrates the depth-first search being utilized to "solve" a maze:
http://nullprogram.com/RunMaze/
Happy optimizing!
Depth-first Searching: this search method basically takes your search through a tree as far in as possible. If there aren't any "priorities", the depth first search will mindlessly delve deeper and deeper until it hits a dead end. In the picture that follows, there is a comparison of the depth-first and breadth-first search method. Take note of how even though Node A branches into several other nodes, the search only returns to it after it has reached a deadend.
Breadth-first Search: contrary to a depth-first search which ignores all other branches from a node and returns them later, a breadth-first search explores all branches from one node before moving on to another, in order of priority if such exists. Again, note the image comparing the two search methods.
(Click to see image in full-size)

A possible application for this would be an automated maze generator/solver. Both work in essentially the same way. The program would simply randomly generate paths in a random direction and if i collides with terrain (computer limits), it will return to its previous starting point and generate in a different direction. For the maze solver, the program would explore the path uniformly until it hits a deadend and returns to the last split-point and explore the other way. In terms of mazes, the optimal search method for a solution would be the breadth-first search. Logically this makes sense because if the program chooses the wrong path, it will return to that node quicker and wind up on the right path than if it had been utilizing a depth-first search, in which case it would end up far deeper in the wrong direcion before it turns around.
This is a relatively interesting way of applying optimization that involves no calculus. In terms of mazes, we usually conduct our own breadth-first seach in our heads, mentally scanning the maze for possible dead ends and avoiding them. So get out those pencils and thinking caps!
Here's a link to an online program that demonstrates the depth-first search being utilized to "solve" a maze:
http://nullprogram.com/RunMaze/
Happy optimizing!
Thursday, February 2, 2012
Optimization: Day IV - V (Lagrange Multipliers)
Today, we continued our unit on optimization problems, and worked with a new method of finding the maxima and minima of functions given a constraint: the Lagrange Multiplier.
The key to Lagrange's method is to picture the level curves of the constraint at every value, c. If the constraint is not tangent to the curve, that means there is still room to either increase or decrease the values of x and y. Naturally, by this reasoning, the maximum or minimum of the function occurs at the point(s) of tangency.
To solve a problem using the Lagrange Multiplier, gradients must be used. Take the gradient of your objective function (the function you are trying to maximize or minimize), as well as the gradient of your constraint, after moving all variables and constants to one side of the equation.
One of the key things to include, now, is the multiplier itself: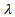
The way this is incorporated with the two gradients is the following, assuming f(x) is the objective function and g(x) is the constraint:
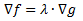
The reason for this can be explained by one word: tangent. When dealing with surfaces, two surfaces are considered "tangent" when their gradients are parallel. This is true when the gradient vectors are either the same, or are scalar multiples of each other. And that scalar multiple is exactly what the Lagrange Multiplier is.
The rest is simple. Distribute the multiplier into the gradient of g(x); set the x values of each vector equal to each other and solve for the multipler--do the same for the y-values.
Plug the multiplier back into the constraint, and solve for x and y. To confirm that your point is really either the maximum or minimum, choose any point that satisfies the constraint--other than the point you found--and see whether is greater or less than the function value of the point derived by the Lagrange Multiplier.
Happy optimizing!
The key to Lagrange's method is to picture the level curves of the constraint at every value, c. If the constraint is not tangent to the curve, that means there is still room to either increase or decrease the values of x and y. Naturally, by this reasoning, the maximum or minimum of the function occurs at the point(s) of tangency.
To solve a problem using the Lagrange Multiplier, gradients must be used. Take the gradient of your objective function (the function you are trying to maximize or minimize), as well as the gradient of your constraint, after moving all variables and constants to one side of the equation.
One of the key things to include, now, is the multiplier itself:
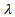
The way this is incorporated with the two gradients is the following, assuming f(x) is the objective function and g(x) is the constraint:
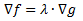
The reason for this can be explained by one word: tangent. When dealing with surfaces, two surfaces are considered "tangent" when their gradients are parallel. This is true when the gradient vectors are either the same, or are scalar multiples of each other. And that scalar multiple is exactly what the Lagrange Multiplier is.
The rest is simple. Distribute the multiplier into the gradient of g(x); set the x values of each vector equal to each other and solve for the multipler--do the same for the y-values.
Plug the multiplier back into the constraint, and solve for x and y. To confirm that your point is really either the maximum or minimum, choose any point that satisfies the constraint--other than the point you found--and see whether is greater or less than the function value of the point derived by the Lagrange Multiplier.
Happy optimizing!
Subscribe to:
Comments (Atom)


































