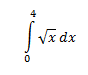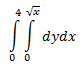Multiple Integration - Double w/ Polar

There are many things that can complicate the process of integration. For instance, what makes the first of the following integrals more daunting than the second?

Well, you wouldn't be wrong if you said the square root. However, when we deal with circular regions, we have no choice but the work with square roots. But what if we could make our lives simpler by moving to another coordinate system--namely, polar? As it turns out, polar makes integrating circular regions that seem overly complicated in rectangular coordinates seem trivial!

But first, it's essential to keep some basic rectangular to polar conversions in mind:

Now, remember our general formula for double integrals?

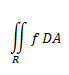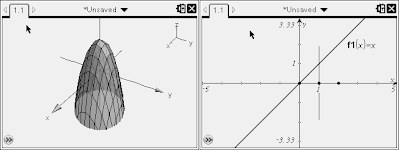
The DA in polar becomes not dydx, like in rectangular coordinates, because the x and y axes only exist in rectangular. In polar, we describe curves by their angle and radius! That's why in polar...

So as a quick example, lets say we're trying to find the volume of the paraboloid x^2+y^2 = z over this circle:

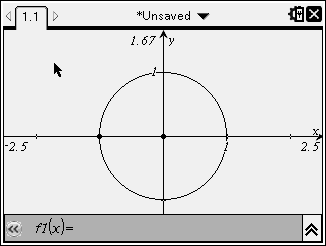Well, we can establish the limits of integration of our area by describing the angle and the radius. The circle runs all the way around, so it extends from 0 to 2pi. The radius is 1.

Note: Double integration for polar coordinates puts the angle first, then the radius.

So our integral would look like:

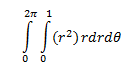
Remember that you also need to convert the equation of the paraboloid (x^2 + y^2) to polar as well, and then tack on the DA.

Happy polar integrating!

Multiple Integration - Double

Before multivariate calculus, many of us should have learned integration in two-dimensions, which essentially finds the area under a curve, constrained by certain limits. In three-dimensions, it's not the area under a curve we want, but rather, the volume. Therefore, it's only natural to think that we'd need a second integral to make it 3D. Below, you can see the general formula for a double integral:

In the equation, R, which applies to both integral signs, is the area over which you are integrating. Take a look at the following image, which displays the graph of the square root of x under certain constraints:

Our first instinct when asked to find the area under the curve may be as follows:

And that would yield the correct answer. However, we can express this as a double integral by "un-evaluating" the function. To do this, simply describe the region in terms of x and y.

• X ranges from 0 to 4
• Y ranges from 0 to sqrt x.

The first region described is entered in the first integral, and the second is inserted in the second. Following that rule, we get:

Now, this may seem trivial--why would anyone want to complicate an integral further by adding another one? Well, what if you were asked to find the volume under a curve over a certain area in the plane? As it turns out, double integrals make this very easy. For instance, the following curve over the adjacent area:

Simply describe the area of integration: x ranges from 0 to 1; y ranges from 0 to x, and double-integrate the paraboloid of x^2 + y^2 according to those limits dydx to get your answer!

Happy double integrating!