Multiple Integration - Double

Before multivariate calculus, many of us should have learned integration in two-dimensions, which essentially finds the area under a curve, constrained by certain limits. In three-dimensions, it's not the area under a curve we want, but rather, the volume. Therefore, it's only natural to think that we'd need a second integral to make it 3D. Below, you can see the general formula for a double integral:

In the equation, R, which applies to both integral signs, is the area over which you are integrating. Take a look at the following image, which displays the graph of the square root of x under certain constraints:

Our first instinct when asked to find the area under the curve may be as follows:

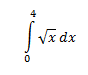And that would yield the correct answer. However, we can express this as a double integral by "un-evaluating" the function. To do this, simply describe the region in terms of x and y.

• X ranges from 0 to 4
• Y ranges from 0 to sqrt x.

The first region described is entered in the first integral, and the second is inserted in the second. Following that rule, we get:

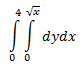Now, this may seem trivial--why would anyone want to complicate an integral further by adding another one? Well, what if you were asked to find the volume under a curve over a certain area in the plane? As it turns out, double integrals make this very easy. For instance, the following curve over the adjacent area:

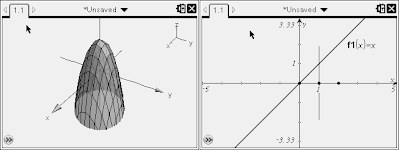Simply describe the area of integration: x ranges from 0 to 1; y ranges from 0 to x, and double-integrate the paraboloid of x^2 + y^2 according to those limits dydx to get your answer!

Happy double integrating!