Tree Searching - Class Presentation

Tree searching is essentially a method of getting from point A to point B. There are two ways to conduct a tree search: one way generates many different results at once while another locates information related to one node first. This seems confusing, but please bear with the text till the end and things may become clearer to you.

Depth-first Searching: this search method basically takes your search through a tree as far in as possible. If there aren't any "priorities", the depth first search will mindlessly delve deeper and deeper until it hits a dead end. In the picture that follows, there is a comparison of the depth-first and breadth-first search method. Take note of how even though Node A branches into several other nodes, the search only returns to it after it has reached a deadend.

Breadth-first Search: contrary to a depth-first search which ignores all other branches from a node and returns them later, a breadth-first search explores all branches from one node before moving on to another, in order of priority if such exists. Again, note the image comparing the two search methods.

(Click to see image in full-size)


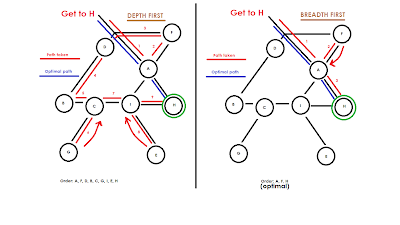
A possible application for this would be an automated maze generator/solver. Both work in essentially the same way. The program would simply randomly generate paths in a random direction and if i collides with terrain (computer limits), it will return to its previous starting point and generate in a different direction. For the maze solver, the program would explore the path uniformly until it hits a deadend and returns to the last split-point and explore the other way. In terms of mazes, the optimal search method for a solution would be the breadth-first search. Logically this makes sense because if the program chooses the wrong path, it will return to that node quicker and wind up on the right path than if it had been utilizing a depth-first search, in which case it would end up far deeper in the wrong direcion before it turns around.

This is a relatively interesting way of applying optimization that involves no calculus. In terms of mazes, we usually conduct our own breadth-first seach in our heads, mentally scanning the maze for possible dead ends and avoiding them. So get out those pencils and thinking caps!

Here's a link to an online program that demonstrates the depth-first search being utilized to "solve" a maze:

http://nullprogram.com/RunMaze/

Happy optimizing!