Optimization: Day IV - V (Lagrange Multipliers)

Today, we continued our unit on optimization problems, and worked with a new method of finding the maxima and minima of functions given a constraint: the Lagrange Multiplier.

The key to Lagrange's method is to picture the level curves of the constraint at every value, c. If the constraint is not tangent to the curve, that means there is still room to either increase or decrease the values of x and y. Naturally, by this reasoning, the maximum or minimum of the function occurs at the point(s) of tangency.

To solve a problem using the Lagrange Multiplier, gradients must be used. Take the gradient of your objective function (the function you are trying to maximize or minimize), as well as the gradient of your constraint, after moving all variables and constants to one side of the equation.

One of the key things to include, now, is the multiplier itself:

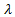
The way this is incorporated with the two gradients is the following, assuming f(x) is the objective function and g(x) is the constraint:



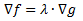
The reason for this can be explained by one word: tangent. When dealing with surfaces, two surfaces are considered "tangent" when their gradients are parallel. This is true when the gradient vectors are either the same, or are scalar multiples of each other. And that scalar multiple is exactly what the Lagrange Multiplier is.

The rest is simple. Distribute the multiplier into the gradient of g(x); set the x values of each vector equal to each other and solve for the multipler--do the same for the y-values.

Plug the multiplier back into the constraint, and solve for x and y. To confirm that your point is really either the maximum or minimum, choose any point that satisfies the constraint--other than the point you found--and see whether is greater or less than the function value of the point derived by the Lagrange Multiplier.

Happy optimizing!