Center of Mass - Double and Triple Integration

All this integrating can be tied together in center of mass. Imagine you have a cube that's gets denser as you move further out towards its corners. Where would it's "center of mass" or "core" be? That can be easily accomplished using multiple integration!

• If it's a 2D surface, use a double integral.
• If it's a 3D volume, use a triple integral.

First, lets describe the mass of a volume. In general, the formula for the mass of a given solid is:

To describe "x ranges" and "y ranges" for centers of mass, these ranges are described as "moments"--how the object acts in a certain direction, literally, at a certain moment in time. The general formulas for these are different for 2D and 3D objects. But the rules are somewhat similar.

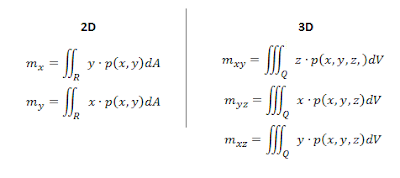Notice that the main difference here is that instead of just having the surface vary along two axes, in 3D space, the object can vary along planes. Also, notice how within the integral, the function of density p(x,y,z) is being multiplied by an additional variable (either x, y, or z). Conveniently, by dividing these moments by the mass, you get one component of the center of mass. Put the components together and you'll get the coordinate of the center of mass for that particular surface or solid!

Happy integrating!