Multiple Integration - Cylindrical Coordinates

Having new coordinate systems to work with may seem at first like an excess of information, but in some cases in mathematics, having another coordinate system to work with can actually make a difficult problem much easier.

Imagine cylindrical coordinates as the polar plane extruded along the z-axis. (Infinitely up and down). By this logic, the three components of cylindrical coordinates are:

This z-component makes all the difference. In polar coordinates, r=3 yields a circle with radius 3. In cylindrical, you get exactly what its name implies—a cylinder of radius 3. It's the circle we had in polar extruded infinitely in the z-direction.

But how do we integrate in cylindrical? Similar to how when we converted our dA or dV in rectangular integration to polar, we get an r with our differentials, in cylindrical integration, we get:

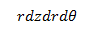Simply express "theta" and the radius (r) as you would in polar. But now, you simply include the z-range and integrate the function accordingly.


To convert between rectangular and cylindrical, refer to the conversions mentioned in the March post: "Multiple Integration - Double w/ Polar".


Happy integrating in cylindrical!