Multivariate Calculus: Polar Integration

In class today, we derived a formula to find the area bounded by a polar graph by tweaking our method of computing the integral under a curve in rectangular coordinates. Instead of using rectangles and finding the Riemann sum, we used sectors, and eventually got:

A = $\frac12\int_a^b r^2\,d\theta.$

The usage of sectors is preferred in the polar coordinate system simply because it is more convenient. We graph polar equations based on circles and angles, whereas in the rectangular system, we use rectangles and defined horizontal and lateral units.

A point to keep in mind:

Note how we have to square the polar function (r) before we integrate. This often results in squaring sine or cosine, which are inconvenient functions to integrate. Luckily, we have trig identities.

cos 2x = cos² x - sin² x

cos 2x = 1 - 2sin² x

cos 2x = 2cos² x - 1

The first identity won't be used as much, as it contains both cosine and sine. The second and third identities have sin² x and cos² x isolated with cos(2x). Do a little algebra and you get:

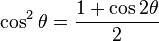
$\cos^2\theta = \frac{1 + \cos 2\theta}{2}\!$