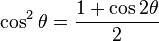Gradient

We discussed the gradient of a function of two variables yesterday.

Definition:
Let f(x,y) have continuous partial derivatives. The gradient of f(x,y) is the vector:

Another notation is grad f(x,y).

Alternative Form of the Directional Derivative (Using gradient):
There is an alternate way to get the directional derivative using the gradient of a function. If f is a differentiable function of x and y, then the directional derivative of f in the direction of the unit vector u is:

Important Properties of the Gradient:

1. If the gradient of the function is 0, then the directional derivative is 0 for all u.

2. The direction of maximum increase of f is given by the gradient of the function. The maximum value of the directional derivative is the magnitude of the gradient of the function.

3. The direction of minimum increase of f is given by the negative gradient of the function. The minimum value of the directional derivative is the magnitude of the gradient of the function.

Directional Derivatives Using Angles

We continued discussing directional derivatives today. After recalling how the formula for the directional derivative is given by:

where f(x,y) is a function of two variables and vector (a,b) is a unit vector, we noticed how it is not always necessary to take the directional vector and unitize it only to plug in variable values based on what point we are taking the derivative at. We can use angles instead.

How does this work? When we originally used vectors, we had vectors such as:

unitized it into:

found the partial derivatives with respect to each variable, and multiplied it out to get the directional derivative, according to the above mentioned formula.

If we use angles, our vector now looks like:

and quite conveniently, any value of theta plugged into this 'angle vector' will also be a unit vector. This can be easily proven by finding the magnitude of u.


Another convenient property of this 'angle vector' is that no point is necessary. The angle value implies movement in a certain direction along both the x and y-axes.

Happy deriving!

Directional Derivative

The definition of the directional derivative is:

By making things simpler, we arrive at:
Let vector u = be a unit vector, then,

And if we choose to make f a function of x, y, and z, then we can write the directional derivative as:

Linear approximation & Total differentials

Back when the Ancient Greeks didn't have calculators, they relied on a method called linear approximation to help estimate the values of functions. Ever wonder how our modern calculators do it? Probably the same way! By constructing a tangent line, we can approximate the value of an unknown point when given the value of a known point. The formula we've all seen last year is:





Now when we extend this to a 3-dimensional space, we construct a plane tangent to the function. This can be summarized by:

f(x+Δx,y+Δy) = f(x,y) + fx (x,y)Δx + fy (x,y)Δy

One example we did in class is:

f(x,y) = x^2+3xy-y^2
Find: f(2.05, 2.96) Known: f(2,3)
Therefore, Δx = 0.05 and Δy = .04

fx = 2x+3y f(x+Δx,y+Δy) = f(x,y) + fx (x,y)Δx + fy (x,y)Δy
fy = 3x-2y 13+0.05(13)-0.04(0) = 13.65



The total differential of a function is the sum of all the partial derivatives. Total differentials can help estimate the maximum error (Δf) in using the differential. It can be summarized by:

z = f(x,y)
dz = fx (x,y)dx + fy (x,y)dy OR Δz = fx (x,y)Δx + fy (x,y)Δy

the curvy d vs. d

Today in class we saw how confusing and intimidating the partial derivative can look when used as a result of the chain rule.

A recap of the difference between the derivative and the partial derivative.:

If w is a function of x and y, and x and y are functions of t, then w is essentially a function if t. That is why we can find the derivative of w with respect to t.
Using the chain rule, we arrive at this formula:

However, if w is a function of x and y, and x and y are functions of s and t, we can no longer find the derivative of w with respect of t. We can find the partial derivative of w with respect to t and s.

Parametric Integration

On Friday, we finished up 2-dimensional integration by looking at how to integrate parametric functions. Noticing how the standard parametric function is denoted as:

we determined that the formula for integration:

can be rewritten as:

by simple substitution.

We proceeded to looking at some problems. One of the more interesting ones was the parametric curve:

which looks like this:

We found that the function crosses the x-axis at t = sqrt 3. After integrating using our new formula to find the area bounded by the curve, we also discovered that the integral from t = -sqrt 3 to t = sqrt 3 was negative. Not only that, but 2x the integral from t = 0 to t = sqrt (3), which we thought would yield the correct answer, was also negative.

We got these results for two reasons, one for each end.

• When we integrated from t = 0 to t = sqrt 3, we were integrating the area denoted by green. As we know, the area under the x-axis is negative, resulting in a negative area when we multiplied by 2.
• When we integrated from t = -sqrt 3 to t = sqrt 3, two things happened:

1. For the first half, from t = -sqrt 3 to 0, we were integrating the function 'backwards', denoted by the red arrow.

2. The second half, from t = 0 to t = sqrt 3, we integrated the green area, which was already established to be negative.

What we gleaned from this problem is that when integrating parametric functions, both the "direction" of integration and the location of the area we are integrating (whether above or below the x-axis) must be taken into consideration.

Happy integrating!

Finding the Area of a Region Between Two Curves

Here is an example of finding an area between two curves without integrating:

Polar Integration

In class today, we derived a formula to find the area bounded by a polar graph by tweaking our method of computing the integral under a curve in rectangular coordinates. Instead of using rectangles and finding the Riemann sum, we used sectors, and eventually got:

A =

The usage of sectors is preferred in the polar coordinate system simply because it is more convenient. We graph polar equations based on circles and angles, whereas in the rectangular system, we use rectangles and defined horizontal and lateral units.

A point to keep in mind:

• Note how we have to square the polar function (r) before we integrate. This often results in squaring sine or cosine, which are inconvenient functions to integrate. Luckily, we have trig identities.

cos 2x = cos² x - sin² x

cos 2x = 1 - 2sin² x

cos 2x = 2cos² x - 1

The first identity won't be used as much, as it contains both cosine and sine. The second and third identities have sin² x and cos² x isolated with cos(2x). Do a little algebra and you get:

and

These identities are useful simply because integrating cos(2x) is a lot easier than cos² x and sin² x.

Happy integrating!

Polar Graphs Using Geogebra

On November 24th, we had a worksheet where we investigated the consequences of changing the parameters in a few basic polar equations (such as r = a sin Θ). Mr. Honner showed us these polar graphs in Geogebra and I'm going to show the "evolution" of Limacons when the parameters are changed in Geogebra also.


Limacons (r = a + b cos Θ):

As I played around with Geogebra, I found out a few things:

As the ratio of a/b increases, the polar graph looks more circular.

• First polar graph: the polar graph has a loop inside itself. The ratio of a/b is 1/2.
• Second polar graph: the polar graph makes a heart shape; there is no loop. The ratio of a/b here is 1.
• Third polar graph: the graph here is getting more circular. The ratio of a/b is 1.33.
• Fourth polar graph: the graph is getting even more circular. The ratio of a/b is 4.

Perhaps we can state it in more general terms:

When a/b is between 0 and 1, the graph will have a loop.

When a/b is 1, the graph will make a "heart."

When a/b is between 1 and 2, the graph will be slightly more circular and have a little "dent."

When a/b is greater than or equal to 2, the graph will be nearly circular.