Multiple Integration - Triple

Triple integration may seem like you're just sticking another integral sign onto a double integral, but it comes with its own set of complications. Similar to how in double integration, you could reverse the order of integration (either dydx or dxdy), in triple integration, you have an array of six possible orders to integrate. For this reason, it is imperative to sketch surfaces properly and keep your limits of integration organized. For instance, suppose you have the plane x + y + z = 1 in the first octant.

Lets describe the volume bounded by the plane in the first octant in the order dzdydx. This essentially means describe how x varies, then y, then z.

• Well, the range for x is easy: from 0 to 1.
• While x ranges from 0 to 1, y ranges from 0 to the line y=x, so from 0 to x.
• And while y ranges from 0 to x, z ranges from 0 to the plane, so from 0 to 1-x-y.

Thus, our triple integral looks something like:

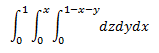
Now what if we switched the order of integration to dxdydz? Well, now we look at z first, then y, then x last.

• Z ranges from 0 to 1.
• This is where the change comes in. As z varies, y doesn't go out to the plane because our "depth" here is the x-coordinate and we haven't described that yet. To determine the limits on the y-axis, we have to look at the trace of the plane.

• Therefore, y ranges from 0 to 1 - z.
• And x ranges from 0 to the plane, so from 0 to 1 - y - z.

Thus, our triple integral in this new order is:

Remember that order matters!

Happy triple integrating!